In the atomic nuclear model discussed in this website (and in entangledenergy.net), nucleon size depends on its energy level, position in the gravitational energy gradient, and level of entanglement with its other nucleon partner as well as its entanglement with its orbital partner. Nucleons, like all other energy, come in discrete units. In this model, nucleons exist as multiples of proton mass-energy:
1 X proton mass (1x pm), 2 X proton mass (2x pm), or 3 X proton mass (3x pm).
Energy sublevels, such as s, p, d, or f, may form ‘separate structures’ with their own set of quantum properties. For example, a ‘p’ energy sublevel (or energy sub-shell) may be filled with six identical nucleons. The six nucleons will each have their own ‘spin’ and each of the orbitals will have its own ‘net’ spin. But all three orbitals with their six nucleons may act together to form a ‘separate structure’ that acts as a single energy entity with its own ‘spin’ and other quantum properties, just as if it was one particle, not six.
There are cases in which not all of the nucleons in an energy sublevel are identical, but still may for a ‘separate structure’ that acts as a single energy entity. Generally, this may happen if there is some sort of symmetry or balance to the arrangement of particles occupying the orbital(s) in that energy sublevel. The ‘separate structure’ in this case will act as a fermion with a spin of 1/2. This will be discussed in more detail below.
If an energy subshell is completely filled with identical particles (e.g., all 2x pm), then its particles will possess alternating e-m directionality and interchanging identities with every e-m interaction. Interchanging identities are important in that one nucleon partner is not distinguishable from another nucleon partner, allowing them to act as an ‘optimal’ boson. In other words, it is not just identical opposing spins that contribute to the formation of ‘optimal’ bosonic behavior.
If an energy subshell is completely filled, but one or more of its constituent nucleons possess more mass-energy (e.g., 3x pm) than other nucleons (e.g. 2x pm) in that subshell, then that subshell will not act as an ‘optimal’ boson, since all its nucleons are not identical, and therefore cannot interchange identities with every e-m interaction (even though they can alternate e-m directionality with every e-m interaction and be at least partially entangled with each other). So, in this case, the nucleons are distinguishable from each other. As a result, if the orbitals in an energy sublevel form a ‘separate structure,’ that structure will act as a fermion.
Likely to form a ‘separate structure:’
Energy sublevels (e.g., s, p, d, and f) in which all orbital(s) are filled with identical particles. The orbital(s) and their nucleons may form a ‘separate structure’ that acts as a boson with an integer spin (e.g., 0, 1)
Example:
Energy sublevels in which each orbital is filled with half one kind of particle (e.g., nucleon = 2x pm) and another kind of particle (e.g., nucleon = 3x pm). The non-identical particles in each orbital may be partially entangled with each other due to differing rates of e-m interaction even though they have other properties in common, such as spin = ½. The symmetry of the orbitals and their nucleons may allow the formation of a ‘separate structure’ that acts as a fermion with a spin of ½.
Example: In the example below, each 3d orbital possesses one 2 X proton mass nucleon and one 3 X proton mass nucleon. The 3 d orbitals may form a separate structure that will act as a fermion since the orbitals consist of non-identical particles. Since the 4s orbital consists of identical particles, it will form a separate structure that acts as a boson.
Energy sublevels in which each orbital is occupied by one identical nucleon. Since the orbitals are not filled, the lone identical nucleons in such an energy level may form a ‘separate structure’ that would act as a fermion with spin = ½.
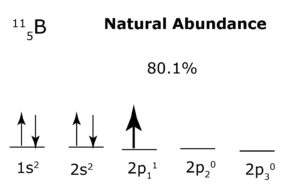
Example: In the example below, the 1s and 2 s orbitals are each filled with identical particles, so each orbital may form a ‘separate structure’ that acts as a boson. On the other hand, each 2 p orbital is occupied by a lone particle, but since each orbital has the same number of particles, and they are all identical, then the 2 p orbitals together may form a ‘separate structure’ that acts as a fermion (since the orbitals are not filled, and therefore not directionally balanced). Note that 2p has an asterisk to show that the lone particles occupying each orbital do not follow Hund’s Rule. This is because each lone particle possesses alternating directionality with every e-m interaction to provide optimal balance to the energy sublevel.
Unlikely to form a ‘separate structure:’
Energy sublevels in which not all of the orbitals are occupied by a particle are unlikely to form a ‘separate structure’ since there is a lack of ‘balance’ or ‘symmetry’ to the energy sublevel.
Example: In the example below, 2 p only has one particle in one of its orbitals. If a second orbital in 2 p also had a particle, this would still leave an empty orbital, so the energy sublevel 2 p would remain unbalanced. So an energy sublevel with empty orbitals will not form a ‘separate structure.’
Energy sublevels in which the orbitals are occupied by a different number of non-identical particles (e.g., nucleons = 3x pm) will not form a ‘separate structure’ since the orbitals of the energy sublevel are not be ‘balanced’ or ‘symmetrical.’
Example: In the example below, the d orbitals are filled with a different amount of 2x pm nucleons and a different amount of 3x pm particles, so the d orbitals will not form a ‘separate structure.’
Hund’s Rule Modified?
One of the purposes of Hund’s Rule is to minimize the probability of the “orbital electrons” of colliding or interfering with each other. If all orbitals of an energy level are all filled with lone electrons with the same spin, there is less probability that they will cross each other’s paths. However, in this model, the orbital particles are not electrons, but electron/positron particles or nucleons, alternating e-m directionality with every e-m interaction. As a result they interchange identities with every e-m interaction as well. They are neither repelled nor attracted to each other, but are entangled and will exist in a region about the center of gravity that will provide optimal directional balance. So in this model, the Modified Hund’s Rule allows the entanglement of lone particles filling successive orbitals within an energy level (such as 3p3).
For orbitals being filled according to Hund’s Rule, in which all lone particles in each orbital possess the same e-m directionality (i.e., all particles are electrons) and spin (i.e., all up or all down), the particles will not be entangled, since entanglement depends on opposing and alternating e-m directionality to maintain directional balance. Under Hund’s Rule, the nucleons possessing the same e-m directionality with the same spins will not be able to form a separate structure since they aren’t entangled with each other. But if they all they all have the same spin, but possess alternating and opposing e-m directionality, they may be partially entangled, and able to form a separate structure that would be a fermion.
Structures that promote the formation of bosons (and energy sublevels)
Bosons may form a number of separate structures at each energy subshell, depending on which type of structure is most stable in that nucleus. The separate structures formed by the nucleon energy subshell orbital may fill 3-D space, but can be reduced to 2-D space to show structural stability (i.e., alternating e-m directionality with adjacent nucleons and with opposing entangled nucleons). Only those structures (with an odd number of orbitals) that result in adjacent particles with opposing e-m directionality when laid out in a 2-D plane will compose stable structures.
All nucleons, regardless of their size (i.e., 1 X proton mass, 2 X proton mass, 3 X proton mass), possess a spin of ½. So an orbital composed of one nucleon = 2X proton mass and one nucleon = 3X proton mass, is a fermion since its constituent particles are not identical, and as a result are distinguishable from each other. While the non-identical nucleons don’t result in optimal directional balance, the orbital nevertheless possesses a net spin of 0, 1.
Rules – Size of nucleons
Nucleons are originally formed in extreme conditions, such as in the cooling of the Big Bang, in plasmas, and inside the cores of stars. They are formed through an interaction of entangled particles and gravitational energy gradient strength. For instance, when a Hydrogen atom, originally consisting of four identical entangled particles goes from a region of extreme hot (or extreme cold) to a region of moderate to cool temperatures, one of its entangled particles moves outward to provide more and more directional balance to the energy system by existing in regions of weaker and weaker gravitational gradient with a higher rate of e-m interaction and corresponding higher rate of time. This, in turn, increases the rate of e-m interaction of its entangled partner within a much stronger gravitational gradient, giving that particle (nucleon) much more mass-energy than its entangled orbital partner.
So the atoms we observe in our cool environment possess nucleons that are significantly larger than their entangled orbital partners. Although they may exist at varying sizes, for simplicity, in this model, only multiples of proton mass will be used for this model. So a nucleon may possess 1 X proton mass-energy, 2 X proton mass-energy, or 3 X proton mass-energy.
If an energy subshell is completely filled with identical particles (i.e., same mass-energy), then the separate structure formed by that subshell is a boson.
If an energy subshell is completely filled, but one or more of its constituent nucleons possesses more mass than other nucleons in that subshell, then that subshell is a fermion since all its constituent particles are not identical.